如图所示,在水平地面上方边长为21的正方形abed区域有方向竖直向上的匀强电场,三角形bcd区域内还有水平向里的匀强磁场。现将一质量0.3kg的物体M以初速度Vo=6m/S从水平地面竖直向上抛出,物体恰能到达bc边中点O,到达O点的瞬间突 然炸裂成质量分别为m1=0.2kg、m2=O.1kg且带等量异种电荷q=0.1C的P、Q两块,炸裂后P在正交电磁场中沿Ob向左做直线运动,Q在正交电磁场中先做匀速圆周运动,然后亦沿水平方向离开正方形区域。已知L=1.2m,重力加速度g=10m/s2,不计空气阻力和P、Q间的库仑力,求:
然炸裂成质量分别为m1=0.2kg、m2=O.1kg且带等量异种电荷q=0.1C的P、Q两块,炸裂后P在正交电磁场中沿Ob向左做直线运动,Q在正交电磁场中先做匀速圆周运动,然后亦沿水平方向离开正方形区域。已知L=1.2m,重力加速度g=10m/s2,不计空气阻力和P、Q间的库仑力,求:
(1) 物体M竖直上抛的最大高度h
(2) 电场强度的大小:
(3)P、Q落到水平地面上的距离。
两个完全相同的物块a、b,在水平面上以相同的初速度从同一位置开始运动,图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象,求:
a、b运动的加速度的大小;
8s末a、b间的距离;
物块的质量。
在光滑的水平面上有一直角坐标。质量为m=4kg的物体,沿y轴正方向以大小为5 m/s的初速度通过坐标原点O,此时给物体施加一个沿x轴正方向的恒力F。一段时间后物体恰好通过点P,P点的坐标为(2.5m,5m)。求:
物体由O运动到P点的时间;
恒力F的大小;
物体在P的速度的大小和方向。
质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速运动,(sin37°=0.6,cos37°=0.8)求:
雪橇对地面的压力大小;
雪橇与水平地面的动摩擦因数的大小.
在地面上方足够高的地方,存在一个高度d=0.5m的“相互作用区域”(下图中画有虚线的部分).一个小圆环A套在一根均匀直杆B上,A和B的质量均为m,若它们之间发生相对滑动时,会产生f=0.5mg的摩擦力.开始时A处于B的最下端,B竖直放置,A距“相互作用区域”的高度h=0.8m.让A和B一起从静止开始下落,只要A处于“相互作用区域”就会受到竖直向上、大小F=3mg的恒力作用,而“相互作用区域”对处于其中的杆B不产生作用力.杆B在下落过程中始终保持竖直,且杆的长度能够保证圆环A与杆不会分离.不计空气阻力,取g=10m/s2.求: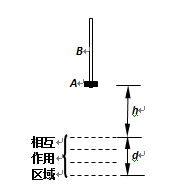
杆B的最下端刚进人“相互作用区域”时的速度;
圆环A通过“相互作用区域”所用的时间;
为保证圆环A在空中运动过程中始终与杆不会分离,杆的最小长度.
水平地面上有一个半径为R的圆形跑道,高为h的平台边缘上P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),P′AOC各点均在同一水平直线上,如图所示.已知重力加速度为g,空气阻力不计,小车可视为质点.则: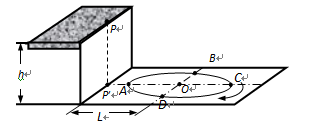
若小车停在跑道上C点时,现从P点水平抛出小沙袋,使其落入小车中,沙袋被抛出时的初速度应为多大?
若小车停在跑道上B点时(∠AOB=90°),现从P点水平抛出小沙袋,使其落入小车中,沙袋被抛出时的初速度为多大?