某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前 后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为
后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为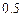 ,
,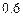 ,
,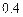 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为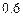 ,
,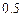 ,
,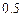 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的 概
概 率;
率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)求甲、乙、丙经过前后两次选拔后,恰有一人合格的概率。
已知椭圆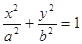 (
(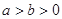 )右顶点与右焦点的距离为
)右顶点与右焦点的距离为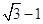 ,短轴长为
,短轴长为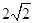 .
.
(I)求椭圆的方程;
(II)过左焦点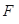 的直线与椭圆分别交于
的直线与椭圆分别交于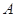 、
、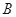 两点,若三角形
两点,若三角形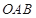 的面积为
的面积为 ,求直线
,求直线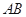 的方程.
的方程.
在四棱锥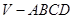 中,底面
中,底面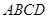 是正方形,侧面
是正方形,侧面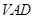 是正三角形,平面
是正三角形,平面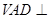 底面
底面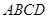 .
.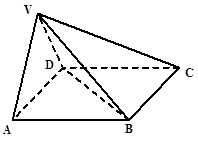
(I) 证明: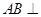 平面
平面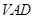 ;
;
(II)求二面角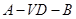 的余弦值.
的余弦值.
其市有小型超市72个,中型超市24个,大型超市12个,现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
(I)求应从小型、中型、大型超市分别抽取的个数;
(II)若从抽取的9个超市中随机抽取3个做进一步跟踪分析,记随机变量X为抽取的小型超市的个数,求随机变量X的分布列及数学期望E(X) .
公差不为零的等差数列{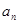 }中,
}中, ,又
,又 成等比数列.
成等比数列.
(I) 求数列{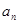 }的通项公式.
}的通项公式.
(II)设 ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.
在锐角 中,
中, ,
,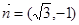 ,
, .
.
(I) 求角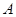 的大小;
的大小;
(II)求 的取值范围.
的取值范围.