其市有小型超市72个，中型超市24个，大型超市12个，现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
（I）求应从小型、中型、大型超市分别抽取的个数；
（II）若从抽取的9个超市中随机抽取3个做进一步跟踪分析，记随机变量X为抽取的小型超市的个数，求随机变量X的分布列及数学期望E(X) .
设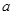
是实数，函数
.
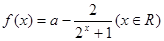（1）试证：对任意，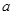
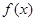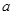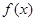在R上为增函数；（2）是否存在，使为奇函数.
设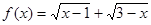
的定义域为A，
，
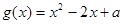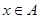的值域为B.
（1）若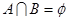
，求实数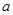
的取值范围；（2）若
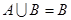，求实数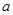的取值范围.
计算：
（1）
（2）已知
，试计算：
.
（本小题满分14分）已知圆C的圆心在坐标原点O，且与直线
相切．
（1）求直线
被圆C所截得的弦AB的长；
（2）若与直线
垂直的直线与圆C交于不同的两点P，Q，且以PQ为直径的圆过原点，求直线的纵截距；
（3）过点G(1,3)作两条与圆C相切的直线，切点分别为M,N，求直线MN的方程．
（本小题满分13分）已知函数
，
集合
，集合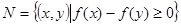
．
（1）求集合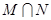
对应区域的面积；
（2）若点
，求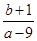
的取值范围．