函数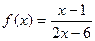 ,
,
用定义证明 在
在 上单调递减;
上单调递减;
若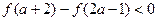 ,求
,求 的取值范围。
的取值范围。
计算以下式子的值:
(1) ;
;
(2)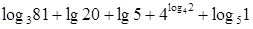 .
.
设函数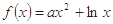 .
.
(Ⅰ)当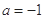 时,求函数
时,求函数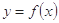 的图象在点
的图象在点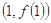 处的切线方程;
处的切线方程;
(Ⅱ)已知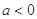 ,若函数
,若函数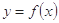 的图象总在直线
的图象总在直线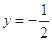 的下方,求
的下方,求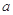 的取值范围;
的取值范围;
已知极坐标系的极点与直角坐标系的原点重合,极轴与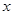 轴的正半轴重合.若直线
轴的正半轴重合.若直线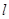 的极坐标方程为
的极坐标方程为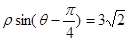 .
.
(1)把直线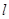 的极坐标方程化为直角坐标系方程;
的极坐标方程化为直角坐标系方程;
(2)已知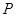 为椭圆
为椭圆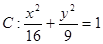 上一点,求
上一点,求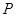 到直线
到直线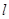 的距离的最大值。
的距离的最大值。
如图,△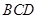 是等边三角形,
是等边三角形, 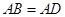 ,
,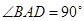 ,
,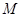 ,
,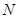 ,
,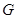 分别是
分别是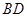 ,
,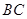 ,
,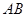 的中点,将△
的中点,将△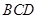 沿
沿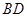 折叠到
折叠到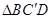 的位置,使得
的位置,使得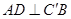 .
.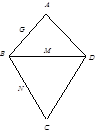
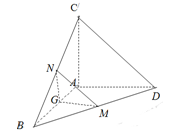
(1)求证:平面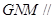 平面
平面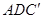 ;
;
(2)求证: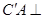 平面
平面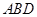 .
.
在直角坐标系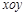 中,直线
中,直线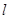 的参数方程为
的参数方程为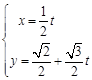 (
(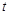 为参数),若以直角坐标系
为参数),若以直角坐标系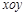 的
的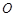 点为极点,
点为极点,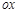 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线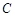 的极坐标方程为
的极坐标方程为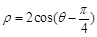 .
.
(1)求直线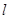 的倾斜角;
的倾斜角;
(2)若直线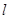 与曲线
与曲线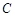 交于
交于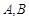 两点,求AB的距离.
两点,求AB的距离.