已知定义在实数集上的函数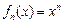 ,
,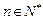 ,其导函数记为
,其导函数记为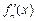 ,且满足:
,且满足: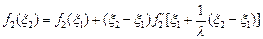
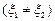 ,
,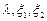 为常数.
为常数.
(Ⅰ)试求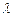 的值;
的值;
(Ⅱ)设函数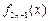 与
与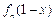 的乘积为函数
的乘积为函数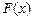 ,求
,求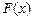 的极大值与极小值;
的极大值与极小值;
(Ⅲ)试讨论关于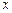 的方程
的方程 在区间
在区间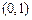 上的实数根的个数.
上的实数根的个数.
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足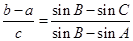 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.
在 中,内角
中,内角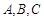 的对边分别为
的对边分别为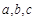 ,且
,且 .
.
(1)求角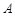 的大小;
的大小;
(2)若 ,求
,求 的面积.
的面积.
在 中,内角
中,内角 、
、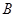 、
、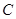 的对边分别为
的对边分别为 、
、 、
、 ,且
,且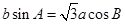 .
.
(1)求角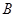 的大小;
的大小;
(2)若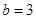 ,
,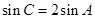 ,求
,求 的面积.
的面积.
在DABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5, .
.
(1) 求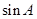 和
和 的值;
的值;
(2) 设函数 ,求
,求 的值.
的值.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知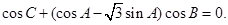
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.