【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱 中有
中有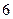 张卡片,其中
张卡片,其中 张写有数字
张写有数字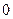 ,
, 张写有数字
张写有数字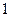 ,
, 张写有数字
张写有数字 ;乙箱中也有
;乙箱中也有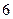 张卡片,其中
张卡片,其中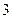 张写有数
张写有数 字
字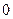 ,
, 张写有数字
张写有数字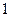 ,
,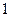 张写有数字
张写有数字 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的 张卡片上数字之积为
张卡片上数字之积为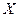 ,求
,求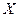 的
的
分布列及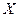 的
的 数学期望;
数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的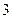 张卡片都写有
张卡片都写有
数字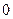 的概率是多少?
的概率是多少?
(本小题满分12分)已知向量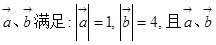 的夹角为
的夹角为 .
.
(1)求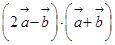 ;(2)若
;(2)若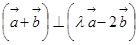 ,求
,求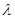 的值.
的值.
(本小题满分12分)函数f(x)=3sin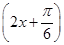 的部分图像如图所示.
的部分图像如图所示.
(1)写出f(x)的最小正周期及图中x0,y0的值;
(2)求f(x)在区间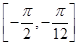 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)设向量a=(4cosα,sinα),b=(sinβ,4cosβ),c=(cosβ,-4sinβ),
(1)若a与b-2c垂直,求tan(α+β)的值;
(2)求|b+c|的最大值.
(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(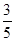 ,
,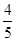 ),记∠COA=α.
),记∠COA=α.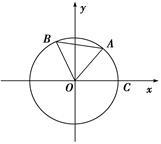
(Ⅰ)求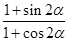 的值;
的值;
(Ⅱ)求cos∠COB的值.
(本小题满分10分)已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.