.如图,等边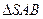 与直角梯形ABCD垂直,
与直角梯形ABCD垂直,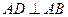 ,
,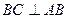 ,
,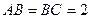 ,
,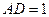 .若E,F分别为AB,CD的中点.
.若E,F分别为AB,CD的中点.
(1)求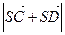 的取值?
的取值?
(2)求面SCD与面SAB所成的二面角大小?
已知抛物线 的焦点
的焦点 以及椭圆
以及椭圆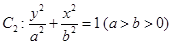 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上.
(1)求抛物线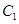 和椭圆
和椭圆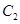 的标准方程;
的标准方程;
(2)过点 的直线交抛物线
的直线交抛物线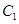 于
于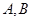 两不同点,交
两不同点,交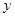 轴于点
轴于点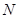 ,已知
,已知 ,求
,求 的值;
的值;
(3)直线 交椭圆
交椭圆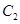 于
于 两不同点,
两不同点, 在
在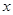 轴的射影分别为
轴的射影分别为 ,
, ,若点
,若点 满足
满足 ,证明:点
,证明:点 在椭圆
在椭圆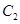 上.
上.
设函数
(1)求f(x)≤6 的解集
(2)若f(x)≥m对任意x∈R恒成立,求m的范围。
设直线 的参数方程为
的参数方程为 (t为参数),若以直角坐标系
(t为参数),若以直角坐标系 的
的 点为极点,
点为极点, 轴为极轴,选择相同的长度单位建立极坐标系,得曲线
轴为极轴,选择相同的长度单位建立极坐标系,得曲线 的极坐标方程为ρ=
的极坐标方程为ρ= .
.
(1)将曲线 的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
(2)若直线 与曲线
与曲线 交于A、B两点,求
交于A、B两点,求 .
.
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证:  ;
;
(2)若AC=3,求 的值。
的值。
已知函数
(Ⅰ)若曲线 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值及函数
的值及函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.