(本小题满分12分)
已知函数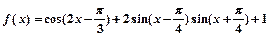
(1)求函数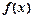 图象的对称轴方程和对称中心;
图象的对称轴方程和对称中心;
(2)求函数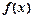 在
在 区间
区间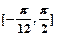 上的值域。
上的值域。
(本小题满分11分)已知函数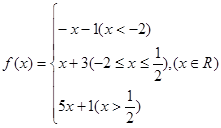
(1)求函数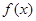 的最小值;
的最小值;
(2)已知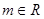 ,命题
,命题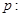 关于
关于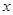 的不等式
的不等式 对任意
对任意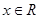 恒成立;命题
恒成立;命题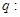 函数
函数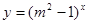 是增函数,若“
是增函数,若“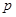 或
或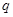 ”为真,“
”为真,“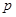 且
且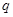 ”为假,求实数
”为假,求实数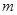 的取值范围.
的取值范围.
设函数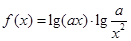 .
.
(1)当a=0.1,求f(1000)的值;
(2)若f(10)=10,求a的值;
(3)若对一切正实数x恒有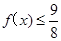 ,求a的取值范围.
,求a的取值范围.
设函数 ,
,
(1)求证:不论 为何实数
为何实数 总为增函数;
总为增函数;
(2)确定 的值,使
的值,使 为奇函数及此时
为奇函数及此时 的值域.
的值域.
已知函数
(1)在给定的直角坐标系内画出 的图象;
的图象;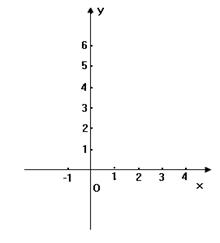
(2)写出 的单调递增区间(不需要证明);
的单调递增区间(不需要证明);
(3)写出 的最大值和最小值(不需要证明).
的最大值和最小值(不需要证明).
已知全集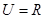 ,集合
,集合 ,
, ,
,
(1)求 、
、 ;
;
(2)若集合 是集合A的子集,求实数k的取值范围.
是集合A的子集,求实数k的取值范围.