(本小题满分10分)
如图,在平面直角坐标系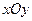 中,以
中,以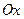 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为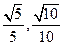 .
.
(1)求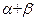 ;
;
(2)求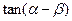 的值.
的值.
已知椭圆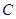 :
: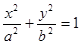
 ,
,
(1)若椭圆的长轴长为4,离心率为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点 的直线
的直线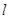 与椭圆
与椭圆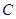 交于不同的两点
交于不同的两点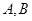 ,且
,且 为锐角(
为锐角(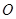 为坐标原点),求直线
为坐标原点),求直线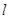 的斜率
的斜率 的取值范围;
的取值范围;
(3)过原点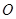 任意作两条互相垂直的直线与椭圆
任意作两条互相垂直的直线与椭圆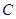 :
: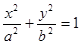
 相交于
相交于 四点,设原点
四点,设原点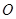 到四边形
到四边形 的一边距离为
的一边距离为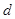 ,试求
,试求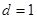 时
时 满足的条件.
满足的条件.
(原创)已知集合M是满足下列性质的函数 的全体:存在非零常数T,对任意
的全体:存在非零常数T,对任意 ∈R,有
∈R,有 成立.
成立.
(1)函数 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)若定义在R上的偶函数 满足
满足 ,求证:
,求证: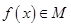 ;
;
(3)设函数 且
且 )的图象与
)的图象与 的图象有公共点,证明:
的图象有公共点,证明: ∈M;
∈M;
在长方体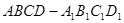 中,
中, ,过
,过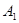 ,
, ,
,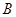 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体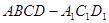 ,这个几何体的体积为
,这个几何体的体积为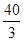 .
.
(1)证明:直线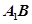 ∥平面
∥平面 ;
;
(2)求棱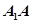 的长;
的长;
(3)在线段 上是否存在点
上是否存在点 ,使直线
,使直线 与
与 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
已知数列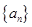 的各项均为正数,其前
的各项均为正数,其前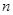 项和为
项和为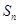 ,且满足
,且满足 ,
,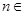 N
N .
.
(1)求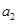 的值;
的值;
(2)求数列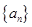 的通项公式;
的通项公式;
(3)是否存在正整数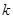 , 使
, 使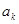 ,
,  ,
, 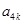 成等比数列? 若存在, 求
成等比数列? 若存在, 求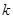 的值; 若不存在, 请说明理由.
的值; 若不存在, 请说明理由.
在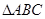 中,
中,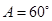 ,
,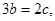
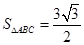 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求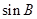 的值.
的值.