已知函数 的定义域为
的定义域为 ,对于任意的
,对于任意的 ,都有
,都有 ,且当
,且当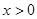 时,
时, ,若
,若 .
.
(1)求证: 为奇函数;
为奇函数;
(2)求证: 是
是 上的减函数;
上的减函数;
(3)求函数 在区间
在区间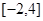 上的值域.
上的值域.
(本小题满分10分)已知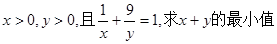 。
。
(本小题满分12分)已知函数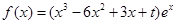 (
(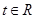 ,
,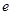 为自然对数的底数)
为自然对数的底数)
(Ⅰ)若函数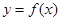 有三个极值点,求
有三个极值点,求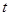 的取值范围
的取值范围
(Ⅱ)若存在实数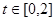 ,使对任意的
,使对任意的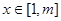 ,不等式
,不等式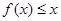 恒成立,求正整数
恒成立,求正整数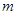 的最大值
的最大值
(本小题满分12分)椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为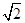 、离心率为
、离心率为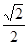 ,直线
,直线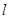 与y轴交于点P(0,
与y轴交于点P(0,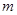 ),与椭圆C交于相异两点A、B,且
),与椭圆C交于相异两点A、B,且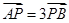 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)求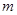 的取值范围。
的取值范围。
(本小题满分12分)已知函数 ,
, ,且
,且 .
.
(Ⅰ)若 ,求
,求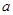 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最大值;
的最大值;
(本小题满分12分)如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是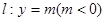 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A。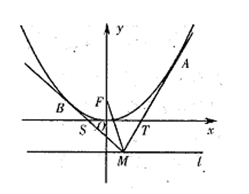
(Ⅰ)求抛物线E的方程;
(Ⅱ)求证:点S,T在以FM为直径的圆上