某厂用鲜牛奶在某台设备上生产
两种奶制品.生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品的产量不超过
产品产量的2倍,设备每天生产
两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量
(单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利 (单位:元)是一个随机变量.

(Ⅰ)求
的分布列和均值;
(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
已知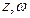 为复数,
为复数, 为纯虚数,
为纯虚数, ,且
,且 .求复数
.求复数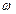 .
.
型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了189名员工进行调查,其中支持企业改革的调查者中,工作积极的54人,工作一般的32人,而不太赞成企业改革的调查者中,工作积极的40人,工作一般的63人.
(1)根据以上数据建立一个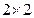 的列联表;
的列联表;
(2)对于人力资源部的研究项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
附表:
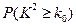 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
设 求证:
求证: (用两种方法证明).
(用两种方法证明).
用三段论证明:通项为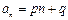 (
( 为常数)的数列
为常数)的数列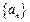 是等差数列.
是等差数列.
(本题满分15分)已知a∈R,函数f (x) =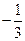 x3 +
x3 +  ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R).(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;(Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由;(Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.