已知二阶矩阵M有特征值 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 。
。
(1)求矩阵M;
(2)求矩阵M的另一个特征值,及对应的一个特征向量e2的坐标之间的关系。
(3)求直线 在矩阵M的作用下的直线
在矩阵M的作用下的直线 的方程.
的方程.
如图的多面体是底面为平行四边形的直四棱柱ABCD— ,经平面AEFG
,经平面AEFG
所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60
(I)求证:BD⊥平面ADG;(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.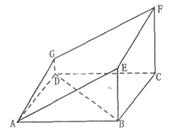
已知=(cosx+sinx,sinx),=(cosx-sinx,2cosx),
(Ⅰ)求证:向量与向量不可能平行;(Ⅱ)若f(x)=·,且x∈[-,]时,求函数f(x)的最大值及最小值
设函数 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若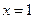 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(即用
的关系式(即用 表示
表示 ),并确定
),并确定 的单调区间;(提示:应注意对a的取值范围进行讨论)
的单调区间;(提示:应注意对a的取值范围进行讨论)
(3)在(2)的条件下,设 ,函数
,函数 .若存在
.若存在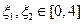 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.
(本小题12分)已知椭圆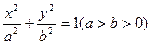 的左右焦点分别为
的左右焦点分别为 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形 是边长为2的正方形。
是边长为2的正方形。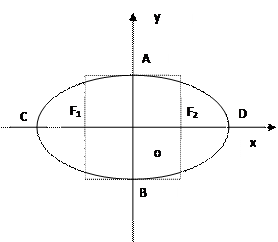
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点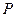 。证明:
。证明: 为定值;
为定值;
(3)在(2)的条件下,试问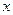 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
第21题图
某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段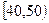 ,
, …
… 后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为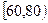 的学生中抽取一个容量为
的学生中抽取一个容量为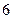 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取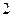 人,求至多有
人,求至多有 人在分数段
人在分数段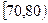 的概率。
的概率。
