已知圆 .
. 
(1)设点 是圆C上一点,求
是圆C上一点,求 的取值范围;
的取值范围;
(2)如图, 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足 求
求 的轨迹的内接矩形的最大面积.
的轨迹的内接矩形的最大面积.
已知函数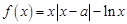 ,
,
 .
.
(Ⅰ)若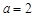 ,求函数
,求函数 在区间
在区间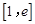 上的最值;
上的最值;
(Ⅱ)若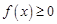 恒成立,求
恒成立,求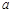 的取值范围.
的取值范围.
注: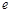 是自然对数的底数
是自然对数的底数
如图,F1,F2是离心率为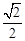 的椭圆C:
的椭圆C: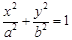 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线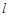 :x=-
:x=-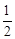 将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.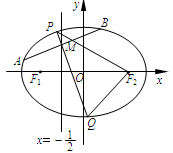
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 求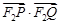 的取值范围.
的取值范围.
如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.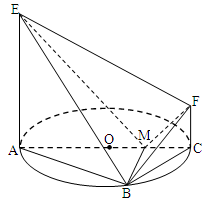
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成锐二面角的余弦值.
在两个不同的口袋中,各装有大小、形状完全相同的1个红球、2个黄球.现分别从每一个口袋中各任取2个球,设随机变量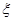 为取得红球的个数.
为取得红球的个数.
(Ⅰ)求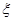 的分布列;
的分布列;
(Ⅱ)求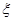 的数学期望
的数学期望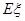 .
.
设公差为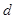 (
(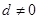 )的等差数列
)的等差数列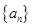 与公比为
与公比为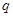 (
(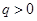 )的等比数列
)的等比数列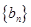 有如下关系:
有如下关系: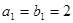 ,
,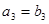 ,
, .
.
(Ⅰ)求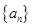 和
和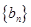 的通项公式;
的通项公式;
(Ⅱ)记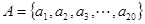 ,
,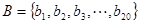 ,
,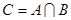 ,求集合
,求集合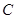 中的各元素之和。
中的各元素之和。