已知函数 ,
, .
.
(I)若函数 在
在 处取得极值,求
处取得极值,求 的单调区间;
的单调区间;
(II)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)
设锐角 的内角
的内角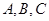 对边的边长分别是
对边的边长分别是 ,
, .
.
(1)求 的大小;
的大小;
(2)求 的取值范围.
的取值范围.
(本小题满分12分)
在△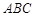 中,已知
中,已知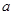 、
、 、
、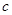 分别是三内角
分别是三内角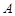 、
、 、
、 所对应的边长,且
所对应的边长,且
(Ⅰ)求角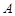 的大小;
的大小;
(Ⅱ)若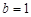 ,且△
,且△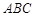 的面积为
的面积为 ,求
,求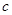 .
.
(本小题满分12分)
已知数列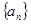 的前
的前 项和为
项和为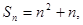
(1)求数列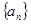 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列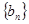 的前
的前 项和
项和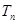 .
.
(本小题满分8分)
已知数列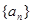 的通项公式
的通项公式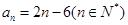 .
.
(1)求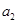 ,
, ;
;
(2)若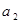 ,
, 分别是等比数列
分别是等比数列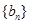 的第1项和第2项,求数列
的第1项和第2项,求数列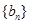 的通项公式
的通项公式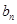 .
.
设数列{ n}满足
n}满足 1=
1= ,
, n+1=
n+1= n2+
n2+ 1,
1,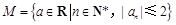 .
.
(Ⅰ)当 ∈(-∞,-2)时,求证:
∈(-∞,-2)时,求证: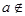 M;
M;
(Ⅱ)当 ∈(0,
∈(0,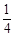 ]时,求证:
]时,求证: ∈M;
∈M;
(Ⅲ)当 ∈(
∈(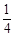 ,+∞)时,判断元素
,+∞)时,判断元素 与集合M的关系,并证明你的结论.
与集合M的关系,并证明你的结论.