在棱长为1的正方体 中,
中, 分别是
分别是 的中点,
的中点,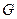 在棱
在棱 上,且
上,且 ,H
,H 为
为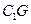 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.
(1)求证: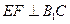 ;
;
(2)求EF与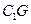 所成的角的余弦;
所成的角的余弦;
(3)求FH的长.
已知抛物线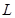 :
: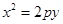 和点
和点 ,若抛物线
,若抛物线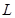 上存在不同两点
上存在不同两点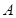 、
、 满足
满足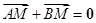 .
.
(1)求实数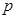 的取值范围;
的取值范围;
(2)当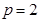 时,抛物线
时,抛物线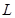 上是否存在异于
上是否存在异于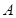 、
、 的点
的点 ,使得经过
,使得经过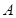 、
、 、
、 三点的圆和抛物线
三点的圆和抛物线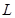 在点
在点 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
如图,四棱锥 中,
中, 平面
平面 ,
, 与底面所成的角为
与底面所成的角为 ,底面
,底面 为直角梯形,
为直角梯形, ,
,
(1)求证:平面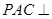 平面
平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使
,使 与平面
与平面 所成的角为
所成的角为 ?若存在,确定点
?若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
已知函数f(x)=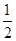 sin2xsinφ+cos2xcosφ-
sin2xsinφ+cos2xcosφ-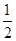 sin
sin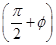 (0<φ<π),其图象过点
(0<φ<π),其图象过点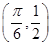 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的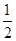 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在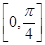 上的最大值和最小值.
上的最大值和最小值.
(1)求不等式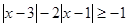 的解集;
的解集;
(2)已知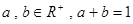 ,求证:
,求证: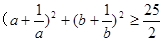 .
.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (t为参数).在极坐标系(与直角坐标系
(t为参数).在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为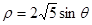
(1)求直线 及圆
及圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线 交于点
交于点 .若点
.若点 的坐标为(3,
的坐标为(3, ),求
),求 .
.