已知椭圆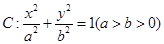 的左、右焦点分别为
的左、右焦点分别为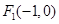 、
、 ,P为椭圆
,P为椭圆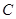 上任意一点,且
上任意一点,且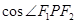 的最小值为
的最小值为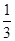 .
.
(1)求椭圆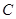 的方程;
的方程;
(2)动圆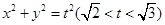 与椭圆
与椭圆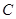 相交于A、B、C、D四点,当
相交于A、B、C、D四点,当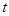 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
设各项为正数的数列 的前
的前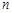 和为
和为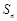 ,且
,且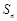 满足:
满足: .等比数列
.等比数列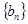 满足:
满足: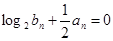 .
.
(Ⅰ)求数列 ,
,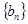 的通项公式;
的通项公式;
(Ⅱ)设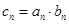 ,求数列
,求数列 的前
的前 项的和
项的和 ;
;
(Ⅲ)证明:对一切正整数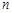 ,有
,有 .
.
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),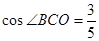 .以
.以 所在直线为
所在直线为 轴,以
轴,以 所在直线为
所在直线为 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求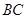 所在直线的方程及新桥BC的长;
所在直线的方程及新桥BC的长;
(Ⅱ)当OM多长时,圆形保护区的面积最大?
并求此时圆的方程.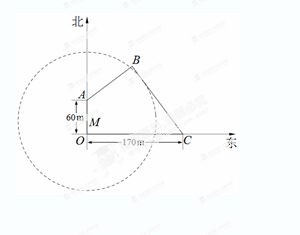
如图,在四棱锥 中,
中,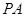 丄平面
丄平面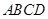 ,
,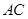 丄
丄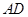 ,
,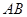 丄
丄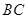 ,
, ,
, ,
, .
.
(Ⅰ)证明: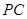 丄
丄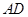 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)求三棱锥 外接球的体积.
外接球的体积.
在直角坐标系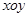 中,已知点
中,已知点 ,
, ,
,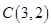 ,点
,点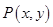 在
在 三边围成的区域(含边界)上,且
三边围成的区域(含边界)上,且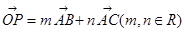 .
.
(Ⅰ)若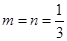 ,求
,求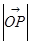 ;
;
(Ⅱ)用 表示
表示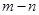 ,并求
,并求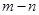 的最小值.
的最小值.
解关于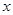 的不等式
的不等式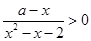 ,其中常数
,其中常数 是实数.
是实数.