已知函数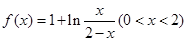 .
.
(1)是否存在点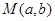 ,使得函数
,使得函数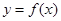 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数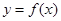 的图像上?若存在,求出点M的坐标;若不存在,请说明理由;
的图像上?若存在,求出点M的坐标;若不存在,请说明理由;
(2)定义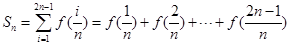 ,其中
,其中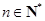 ,求
,求 ;
;
(3)在(2)的条件下,令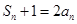 ,若不等式
,若不等式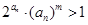 对
对 且
且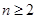 恒成立,求实数
恒成立,求实数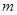 的取值范围.
的取值范围.
如图, 在平面直角坐标系 中, 已知以 为圆心的圆
及其上一点
(1) 设圆 与 轴相切, 与圆 外切, 且圆心 在直线 上, 求圆 的标准方程;
(2) 设平行于 的直线 与圆 相交于 两点, 且 , 求直线 的方程;
(3) 设点 满足:存在圆 上的两点 和 , 使得 , 求实数 的取值范围。

现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱雉 ,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高 的四倍.
(1)若 ,则仓库的容积是多少?
(2)若正四棱柱的侧棱长为 ,则当 为多少时,仓库的容积最大?

如图,在直三棱柱 中, 分别为 的中点,点 在侧棱 上, 且
求证:(1)直线 平面 ;
(2) 平面 平面 ;

(1) 求 的长;
;
已知函数 =│ x+1│-│ x-2│.
(1)求不等式 ≥1的解集;
(2)若不等式 ≥ x 2- x+ m的解集非空,求实数 m的取值范围.