（本小题12分）
在某次高三质检考试后，抽取了九位同学的数学成绩进行统计，下表是九位同学的选择题和填空题的得分情况：
| 选择题 |
40 |
55 |
50 |
45 |
50 |
40 |
45 |
60 |
40 |
| 填空题 |
12 |
16 |
  |
12 |
16 |
12 |
8 |
12 |
8 |
（Ⅰ）若这九位同学填空题得分的平均分为
，试求表中的值及他们填空题得分的标准差；
（Ⅱ）在（Ⅰ）的条件下，记这九位同学的选择题得分组成的集合为
，填空题得分组成的集合为
．若同学甲的解答题的得分是
，现分别从集合、中各任取一个值当作其选择题和填空题的得分，求甲的数学成绩高于
分的概率
(10分)△ABC中，已知三个顶点的坐标分别是A（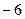
，0），B（6，0），C（6，5），
（1）求AC边上的高线BH所在的直线方程；
（2）求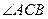
的角平分线所在直线的方程。
（本小题满分12分）设递增等比数列{
}的前n项和为
，且
＝3，
＝13，数列{
}满足
＝
，点P（，
）在直线x－y＋2＝0上，n∈N﹡
（Ⅰ）求数列{
}，{}的通项公式
（Ⅱ）设
＝
，数列{}的前n项和
，若>2a－1恒成立（n∈N﹡），求实数a的取值范围．
（本小题满分12分）
已知半圆x2＋y2＝3（y≥0），P为半圆上任一点，A（2，0）为定点，以P
A为边作正三角形PAB，且点B与圆心分别在PA的两侧，求四边形POAB面积的最大值．
（本小题满分12分）
解不等式x2－x＋a－a2<0．
（本小题满分12分）
△A
BC中，内角A、B、C的对边分别为a、b、c
（I）若△ABC面积
＝
，c＝2，A＝60°，求a，b的值
（Ⅱ）若a＝c·cosB，且b＝c·sinA，试判断△ABC的形状