(本小题满分12分)设递增等比数列{ }的前n项和为
}的前n项和为 ,且
,且 =3,
=3, =13,数列{
=13,数列{ }满足
}满足
 =
= ,点P(
,点P( ,
, )在直线x-y+2=0上,n∈N﹡
)在直线x-y+2=0上,n∈N﹡
(Ⅰ)求数列{
 },{
},{ }的通项公式
}的通项公式
(Ⅱ)设 =
= ,数列{
,数列{ }的前n项和
}的前n项和 ,若
,若 >2a-1恒成立(n∈N﹡),求实数a的取值范围.
>2a-1恒成立(n∈N﹡),求实数a的取值范围.
已知a=(cos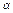 ,sin
,sin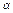 ),b=(cos
),b=(cos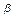 ,sin
,sin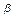 )(0<
)(0<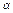 <
<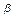 <
<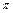 ).
).
(1)求证:a+b与a-b互相垂直;
(2)若ka+b与a-kb的模相等,求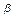 -
-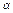 .(其中k为非零实数)
.(其中k为非零实数)
A(2,3),B(5,4),C(7,10), =
= +
+
 .当
.当 为何值时,
为何值时,
(1)点P在第一、三象限的角平分线上;
(2)点P到两坐标轴的距离相等?
在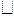 ABCD中,A(1,1),
ABCD中,A(1,1),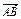 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.
(1)若 =(3,5),求点C的坐标;
=(3,5),求点C的坐标;
(2)当|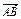 |=|
|=| |时,求点P的轨迹.
|时,求点P的轨迹.
若a,b为非零向量且a∥b,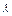 1,
1,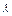 2∈R,且
2∈R,且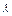 1
1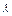 2≠0.
2≠0.
求证: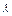 1a+
1a+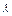 2b与
2b与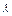 1a-
1a-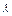 2b为共线向量.
2b为共线向量.
已知A(-2,4),B(3,-1),C(-3,-4).
设 =a,
=a,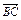 =b,
=b,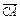 =c,且
=c,且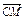 =3c,
=3c,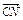 =-2b,
=-2b,
(1)求:3a+b-3c;
(2)求满足a=mb+nc的实数m,n.