(本小题满分12分)
下表是关于某设备的使用年限 (年)和所需要的维修费用
(年)和所需要的维修费用 (万元)的几组统计数据:
(万元)的几组统计数据:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)估计使用年限为10年时,维修费用为 多少?
(参考数值: )
)
选修4-1:几何证明选讲
如图,已知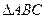 ,过顶点
,过顶点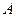 的圆与边
的圆与边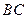 切于
切于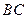 的中点
的中点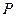 ,与边
,与边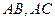 分别交于点
分别交于点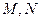 ,且
,且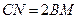 ,点
,点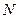 平分
平分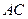 .求证:
.求证: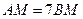 .
.
四、选做题(本小题满分10分。请考生22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分)
22.选修4—4:坐标系与参数方程
求直线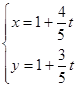 (
(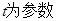 )被曲线
)被曲线 所截的弦长.
所截的弦长.
(本小题满分12分)
已知函数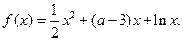
(Ⅰ)若函数 是定义域上的单调增函数,求实数
是定义域上的单调增函数,求实数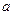 的最小值;
的最小值;
(Ⅱ)方程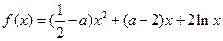 有两个不同的实数解,求实数
有两个不同的实数解,求实数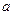 的取值范围;
的取值范围;
(Ⅲ)在函数 的图象上是否存在不同两点
的图象上是否存在不同两点 ,线段
,线段 的中点的横坐标为
的中点的横坐标为 ,有
,有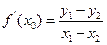 成立?若存在,请求出
成立?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
本小题满分12分)
如图,在四棱柱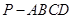 中,底面
中,底面 为直角梯形,
为直角梯形, ,
,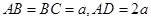 ,
,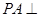 平面
平面 ,
,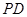 与平面
与平面 成
成 角.
角.
(Ⅰ)若 ,
, 为垂足,求证:
为垂足,求证:
(Ⅱ)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(本小题满分12分)
如图8—3,已知ΔOFQ的面积为S,且 .(1)若
.(1)若 ,求向量
,求向量 与
与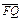 的夹角θ的取值范围;(2)设
的夹角θ的取值范围;(2)设 ,
, ,若以O为中心,F为焦点的椭圆经过点Q,当
,若以O为中心,F为焦点的椭圆经过点Q,当 取得最小值时,求此椭圆方程.
取得最小值时,求此椭圆方程.