为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计 上午8:00 —10:00间各自的点击量,
上午8:00 —10:00间各自的点击量, 得如下所示的统计图,根据统计图
得如下所示的统计图,根据统计图
| |
|
甲 |
|
乙 |
|
|
|
| |
|
8 |
0 |
5 |
6 |
|
|
| |
|
|
1 |
2 |
4 |
9 |
9 |
| 5 |
4 |
0 |
2 |
1 |
|
|
|
| |
|
8 |
3 |
6 |
7 |
|
|
| |
|
1 |
4 |
2 |
2 |
5 |
|
| |
8 |
5 |
5 |
4 |
|
|
|
| 7 |
6 |
4 |
6 |
1 |
|
|
|
| 3 |
2 |
0 |
7 |
|
|
|
|
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎 ?并说明理由。
?并说明理由。
(本小题12分)已知函数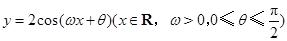 的图象与
的图象与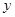 轴相交于点M
轴相交于点M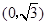 ,
,
且该函数的最小正周期为 .
.
(1)求 和
和 的值;
的值;
(2)已知点 ,点
,点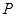 是该函数图象上一点,点
是该函数图象上一点,点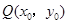 是
是 的中点,当
的中点,当 ,
,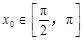 时,求
时,求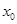 的值。
的值。
(本小题满分12分)已知 为圆
为圆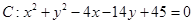 上任一点,且点
上任一点,且点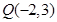 .
.
(1)若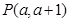 在圆
在圆 上,求线段
上,求线段 的长及直线
的长及直线 的斜率;
的斜率;
(2)求 的最大值和最小值;
的最大值和最小值;
(3)若 ,求
,求 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
(本小题满分10分)已知函数 =
= (2≤
(2≤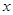 ≤4)
≤4)
(1)令 ,求y关于t的函数关系式,t的范围.
,求y关于t的函数关系式,t的范围.
(2)求该函数的值域.
(本小题满分12分)
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点 (4
(4 ,
,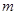 )到焦点的距离为5.
)到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线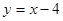 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证: .
.