某污水处理厂预计2010年底投入200万元,购入一套污水处理设备。该设备每年的运转费用是0.5 万元,此外每年都要花费一定的维护费,第一年的维护费为2万元, 由于设备老化,以后每年的维护费都比上一年增加1万元。
由于设备老化,以后每年的维护费都比上一年增加1万元。
(1)求该污水处理厂使用该设备n年 的年平均费用y(万元);
的年平均费用y(万元);
(2)为使该污水处理厂的年平均费用最低,该污水处理厂几年后需要重新更换新的污水处理设备?
五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
分别写出下列命题的逆命题、逆否命题,并判断它们的真假:
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若x2+y2=0,则x,y全为零.
已知函数
(1)若函数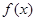 在
在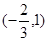 上单调递减,在
上单调递减,在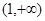 上单调递增,求实数
上单调递增,求实数 的值;
的值;
(2)是否存在实数 ,使得
,使得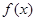 在
在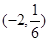 上单调递减,若存在,试求
上单调递减,若存在,试求 的取值范围;
的取值范围;
若不存在,请说明理由;
(3)若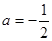 ,当
,当 时不等式
时不等式 有解,求实数
有解,求实数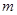 的取值范围.
的取值范围.
已知集合 ,
,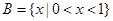 ,
,
(1)若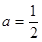 ,求
,求 ;
;
(2)若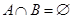 ,求实数a的取值范围.
,求实数a的取值范围.
已知函数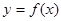 是定义在
是定义在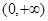 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有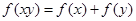 ,且满足
,且满足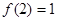 .
.
(1)求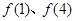 的值;
的值;
(2)求满足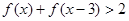 的
的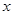 的取值范围.
的取值范围.