．（本小题满分12分）如图，四边形ABCD为正方形，PD平面-优题课

．（本小题满分12分）
如图，四边形ABCD为正方形，PD平面ABCD，PD=AD=2。

（1）求PC与平面PBD所成的角；
（2）在线段PB上是否存在一点E，使得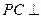平面ADE？并说明理由。

科目数学题型解答题难度中等

已知 $q$ 和 $n$ 均为给定的大于1的自然数，设集合 $M = {0, 1, 2, \dots, q - 1}$ ，集合 $A = {x | x = x_{1} + x_{2} q + \dots x_{n} q^{n - 1}, x_{i} \in M, i = 1, 2, \dots n}$

(1)当 $q = 2, n = 3$ 时，用列举法表示集合A；
(2)设 $s, t \in A, s = a_{1} + a_{2} q + \dots + a_{n} q^{n - 1}, t = b_{1} + b_{2} q + \dots + b_{n} q^{n - 1}$ 其中 $a_{i,} b_{i} \in M, i = 1, 2, \dots n$ 证明：若 $a_{n} < b_{n}$ 则 $s < t$ .

已知函数 $f (x) = x^{2} - \frac{2}{3} a x^{3} (a > 0), x \in R .$

（1）求 $f (x)$ 的单调区间和极值；
（2）若对于任意的 $x_{1} \in (2, + \infty)$ ，都存在 $x_{2} \in (1, + \infty)$ ，使得 $f (x_{1}) \cdot f (x_{2}) = 1$ ，求 $a$ 的取值范围

设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}, F_{2}$ ,，右顶点为 $A$ ，上顶点为 $B$ .已知 $|A B| = \frac{\sqrt{3}}{2} |F_{1} F_{2}|$ .
(1)求椭圆的离心率；
(2)设 $P$ 为椭圆上异于其顶点的一点，以线段 $P B$ 为直径的圆经过点 $F_{1}$ ，经过点 $F_{2}$ 的直线 $l$ 与该圆相切与点 $M$ ， $|M F_{2}| = 2 \sqrt{2}$ .求椭圆的方程.

如图，四棱锥 $P - A B C D$ 的底面 $A B C D$ 是平行四边形， $B A = B D = \sqrt{2}$ ， $A D = 2, P A = P D = \sqrt{5}$ , $E, F$ 分别是棱 $A D, P C$ 的中点.
（1）证明 $: E F / /$ 平面 $P A B$ ；
（2）若二面角 $P - A D - B$ 为 $60^{°}$ ，
①证明：平面 $P B C ⊥$ 平面 $A B C D$ .
②求直线 $E F$ 与平面 $P B C$ 所成角的正弦值.

在 $∆ A B C$ 中,内角 $A, B, C$ 所对的边分别为 $a, b, c$ ,已知 $a - c = \frac{\sqrt{6}}{6} b, \sin B = \sqrt{6} \sin C$ .

（1）求 $\cos A$ 的值；
（2）求 $\cos (2 A - \frac{π}{6})$ 的值.

试卷网试题网古诗词网作文网范文网