(本小题共14分)
已知函数
(1)试用含有a的式子表示b,并求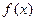 的单调区间;
的单调区间;
(2)设函数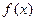 的最大值为
的最大值为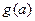 ,试证明不等式:
,试证明不等式:
(3)首先阅读材料:对于函数图像上的任意两点 ,如果在函数图象上存在点
,如果在函数图象上存在点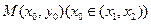 ,使得
,使得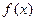 在点M处的切线
在点M处的切线 ,则称AB存在“相依切线”特别地,当
,则称AB存在“相依切线”特别地,当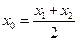 时,则称AB存在“中值相依切线”。
时,则称AB存在“中值相依切线”。
请问在函数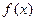 的图象上是否存在两点
的图象上是否存在两点 ,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
(本小题满分12分)
已知函数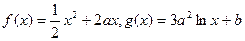 ,
,
(Ⅰ)设两曲线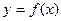 与
与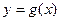 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若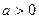 ,试建立
,试建立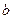 关于
关于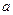 的函数关系式;
的函数关系式;
(Ⅱ)若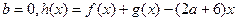 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求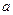 的取值范围.
的取值范围.
(本小题满分l2分)
设椭圆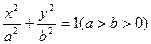 的焦点分别为
的焦点分别为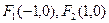 ,直线
,直线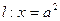 交
交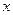 轴于点
轴于点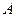 ,且
,且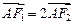 .
.
(Ⅰ)试求椭圆的方程;
(Ⅱ)过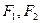 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形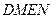 面积的最大值和最小值.
面积的最大值和最小值.
|
本小题满分12分)
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。
( I )求证:AF//平面BCE;
( II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。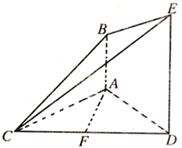
(本小题满分12分)
已知向量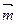 ="(sinA" ,sinB),
="(sinA" ,sinB), =(cosB,cosA),
=(cosB,cosA),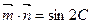 且A、B、C分别为△ABC的三边
且A、B、C分别为△ABC的三边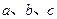 所对的角。
所对的角。
(Ⅰ)求角C的大小;
(Ⅱ)若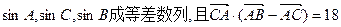 ,求c边的长。
,求c边的长。
(本小题满分12分)
已知 是等差数列,其中
是等差数列,其中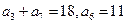 .
.
(Ⅰ)求数列 通项
通项 ;
;
(Ⅱ)若数列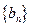 满足
满足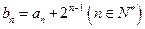 ,求数列
,求数列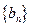 的前
的前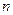 项和
项和 .
.