证明(1)已知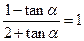 ,求证
,求证
(2)已知数列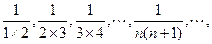 计算
计算 由此推算
由此推算 的公式,并用数学归纳法给出证明。
的公式,并用数学归纳法给出证明。
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是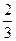 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
已知各项都不相等的等差数列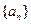 的前6项和为60,且
的前6项和为60,且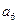 为
为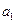 和
和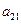 的等比中项.
的等比中项.
( I )求数列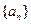 的通项公式;
的通项公式;
(II) 若数列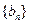 满足
满足 ,且
,且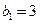 ,求数列
,求数列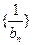 的前
的前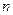 项和
项和 .
.
在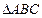 中,
中,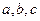 分别是角
分别是角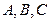 的对边,向量
的对边,向量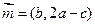 ,
,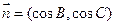 ,且
,且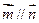 .
.
(Ⅰ)求角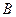 的大小;
的大小;
(Ⅱ)设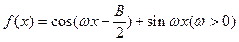 ,且
,且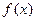 的最小正周期为
的最小正周期为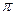 ,求
,求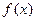 在区间
在区间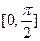 上的最大值和最小值.
上的最大值和最小值.
设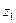 ,
, 为共轭复数,且
为共轭复数,且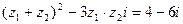 ,求
,求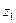 和
和 。
。
已知:如图,⊙O与⊙P相 交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长
交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长 线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2
线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2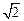 ,求E
,求E F的长.
F的长.