已知椭圆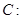
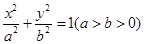 的左焦点为
的左焦点为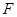 ,左、右顶点分别为
,左、右顶点分别为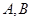 ,过点
,过点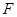 且倾斜角为
且倾斜角为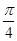 的直线
的直线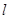 交椭圆于
交椭圆于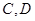 两点,椭圆
两点,椭圆 的离心率为
的离心率为 ,
,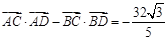 .
.
(1)求椭圆 的方程;
的方程;
(2)若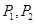 是椭圆上不同两点,
是椭圆上不同两点,
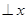 轴,圆
轴,圆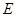 过点
过点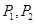 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆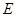 内,则称圆
内,则称圆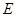 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆 是否存在过点
是否存在过点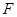 的内切圆?若存在,求出点
的内切圆?若存在,求出点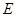 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费
为 元(
元( 为常数,且
为常数,且 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据
),根据
市场调查,销售量 与
与 成反比,当每
成反比,当每 公斤蘑菇的出厂价为30元时,日销售量为100公斤.
公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(1)求该工厂的每日利润 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 元的函数关系式;
元的函数关系式;
(2)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润
 最大,并求最大值
最大,并求最大值
已知函数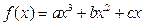 在点
在点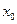 处取得极大值
处取得极大值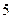 ,
,
其导函数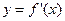 的图象经过点
的图象经过点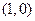 ,
,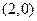 ,如图所示.
,如图所示.
求: (1)
(1)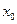 的值;(2)
的值;(2)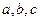 的值.
的值.
(3)、若曲线

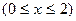 与
与 有两个不同的交点,
有两个不同的交点,
求实数 的取值范围。
的取值范围。
(已知函数 图像上的点
图像上的点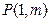 处的切线方程为
处的切线方程为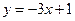 .[来
.[来
(1)若 函数
函数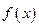 在
在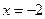 时有极
时有极 值,求
值,求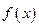 的表达式;
的表达式;
(2)函数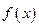 在区
在区 间
间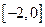 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
计算下列定积分。
(1) (2)
(2) 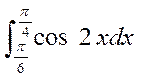 (3)
(3)
一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
| 速度(x转/秒) |
每小时生产有缺点的产品数(y个) |
||
| 8 |
6 |
||
| 9 |
8 |
||
| 10 |
10 |
||
| 13 |
12 |
(1)、画出散点图;
(2)、求机器运转速度与每小时生产有缺点的产品数之间的回归方程;(系数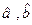 用分数表示)
用分数表示)
(3)、若实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度每秒不超过多少转?