设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n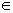 N+,都有
N+,都有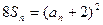 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设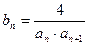 ,
,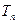 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得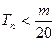 对所有n
对所有n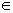 N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某市公安局交通管理部门于2012年1月的某天晚上8点至11点在市区昌隆饭店设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).
|

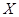 的分布列和数学期望.
的分布列和数学期望.
已知各项都不相等的等差数列 的前6项和为60,且
的前6项和为60,且 为
为 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且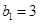 ,求数列
,求数列 的前
的前 项和
项和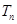
设M是由满足下列条件的函数f(X)构成的集合:
①方程 有实数根;
有实数根;
②函数 的导数
的导数 (满足
(满足 ”
”
(I )若函数 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;
(II)判断函^ 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(III)“对于(II)中函数 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在 ,使得
,使得 ”,请利用函数
”,请利用函数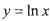 的图象说明这一结论.
的图象说明这一结论.
已知焦点在X轴上的椭圆C为. ,F1、F2分别是椭圆C的左、右焦点,离心率e=
,F1、F2分别是椭圆C的左、右焦点,离心率e=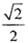 .
.
(I )求椭圆C的方程;
(II) 设点Q的坐标为(1,0),椭圆上是否存在一点P,使得直线 都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.
都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.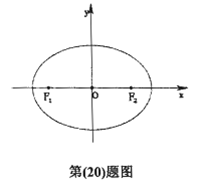
若数列 满足:
满足:
(I) 证明数列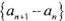 是等差数列;.
是等差数列;.
(II) 求使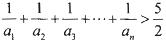 成立的最小的正整数n
成立的最小的正整数n