已知正三角形
的三个顶点都在抛物线
上,其中
为坐标原点,设圆
是
的内接圆(点
为圆心)
(I)求圆
的方程;
(II)设圆
的方程为
,过圆
上任意一点
分别作圆
的两条切线
,切点为
,求
的最大值和最小值.
本小题满分14分)
在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列.
(1)若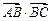 =
=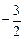 ,b=
,b=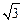 ,求a+c的值;
,求a+c的值;
(2)求 的取值范围.
的取值范围.
(本小题满分16分)
已知数列 满足
满足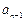 +
+ =4n-3(n∈
=4n-3(n∈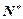 ).
).
(1)若数列 是等差数列,求
是等差数列,求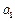 的值;
的值;
(2)当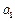 =2时,求数列
=2时,求数列 的前n项和
的前n项和 ;
;
(3)若对任意n∈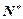 ,都有
,都有 ≥5成立,求
≥5成立,求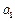 的取值范围.
的取值范围.
(本小题满分16分)
已知函数 =
=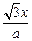 +
+ ,a≠0且a≠1.
,a≠0且a≠1.
(1)试就实数a的不同取值,写出该函数的单调增区间;
(2)已知当x>0时,函数在(0, )上单调递减,在(
)上单调递减,在( ,
, 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;
(3)记(2)中的函数图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出直线l的方程;若不存在,请说明理由.
(本小题满分16分)
已知F是椭圆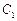 :
: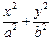 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆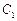 上的动点,点Q是圆
上的动点,点Q是圆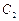 :
: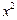 +
+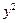 =
=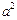 上的动点.
上的动点.
(1)试判断以PF为直径的圆与圆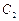 的位置关系;
的位置关系;
(2)在x轴上能否找到一定点M,使得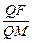 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
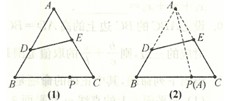
.(本小题满分14分)
如图,在边长为10的正三角形纸片ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形纸片后,顶点A正好落在边BC上(设为P),在这种情况下,求AD的最小值.