((本小题满分13分)
甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名女乒乓球选手,学校计划从甲乙两班各选2名选手参加体育交流活动.
(Ⅰ)求选出的4名选手均为男选手的概率.
(Ⅱ)记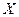 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求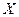 的分布列和期望.
的分布列和期望.
(理科)在平面直角坐标系 中,点
中,点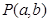
 为动点,
为动点, 分别为椭圆
分别为椭圆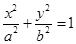 的左右焦点.已知△
的左右焦点.已知△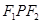 为等腰三角形.
为等腰三角形.
(Ⅰ)求椭圆的离心率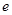 ;
;
(Ⅱ)设直线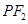 与椭圆相交于
与椭圆相交于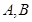 两点,
两点, 是直线
是直线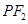 上的点,满足
上的点,满足 ,求点
,求点 的轨迹方程.
的轨迹方程.
(文科)已知椭圆 过点
过点 和点
和点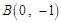 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线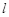 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求直线
,求直线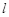 的方程.[来
的方程.[来
(文科)已知中心在原点的双曲线C的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以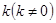 为斜率的直线
为斜率的直线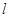 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求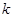 的取值范围.
的取值范围.
(理科)已知动点 在直线
在直线 上,过点
上,过点 分别作曲线
分别作曲线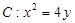 的切线
的切线 ,切点为
,切点为 、
、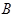 , 求证:直线
, 求证:直线 恒过一定点,并求出该定点的坐标?
恒过一定点,并求出该定点的坐标?
(文科)已知直线 与双曲线
与双曲线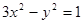 交于
交于 、
、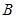 点。
点。
(1)求 的取值范围;
的取值范围;
(2)若以
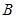 为直径的圆过坐标原点,求实数
为直径的圆过坐标原点,求实数 的值;
的值;
(3)是否存在这样的实数 ,使
,使 、
、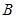 两点关于直线
两点关于直线 对称?若存在,求出
对称?若存在,求出 值;若不存在,说明理由。
值;若不存在,说明理由。