计算: .
.
如图,在直角坐标系中,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为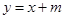 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.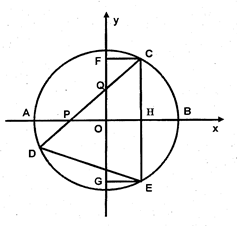
(1)点P在运动过程中,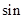 ∠CPB=;
∠CPB=;
(2)当m=3时,试求矩形CEGF的面积;
(3)当P在运动过程中,探索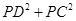 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
(4)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度
十一届全国人大常委会第二十次会议审议的个人所得税法自2011年9月1日起正式实施,新税法将个人所得税的起征点由原来每月2000元提高到3500元,并将9级超额累进税率修改为7级,新旧两种征税方法的1~5级税率情况见下表:
| 税级 |
原征税方法 |
新征税方法 |
||||
| 月应纳税额x |
税率 |
速算扣除数 |
月应纳税额x |
税率 |
速算扣除数 |
|
| 1 |
x≤500 |
5% |
0 |
x≤1 500 |
3% |
0 |
| 2 |
500<x≤2000 |
10% |
25 |
1500<x≤4500 |
10% |
▲ |
| 3 |
2000<x≤5000 |
15% |
125 |
4500<x≤9000 |
20% |
▲ |
| 4 |
5000<x≤20000 |
20% |
375 |
9000<x≤35000 |
25% |
1005 |
| 5 |
20000<x≤40000 |
25% |
1375 |
35000<x≤55 000 |
30% |
2755 |
注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额.
“速算扣除数”是为快捷简便计算个人所得税而设定的一个数.
例如:按原个人所得税法的规定,某人去年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1~3级超额累进税率计算,即500×5%+1500×10%十600×15%=265(元).
方法二:用“月应纳税额x适用税率一速算扣除数”计算,即2600×15%一l25=265(元)。
(1)请把表中空缺的“速算扣除数”填写完整;
(2)甲去年3月缴了个人所得税1060元,若按“新税法”计算,则他应缴税款多少元?
(3)乙今年3月按“新税法”缴了个人所得税2千多元,比去年3月按“原税法”所缴个人所得税少了155元(今年与去年收入不变),那么乙今年3月所缴税款的具体数额为多少元?
如图,在平面直角坐标系中,将一块腰长为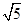 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(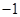 ,0),点B在抛物线
,0),点B在抛物线 上.
上.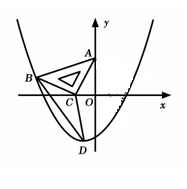
(1)点A的坐标为,点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
各奖项人数百分比统计图各项奖人数统计图
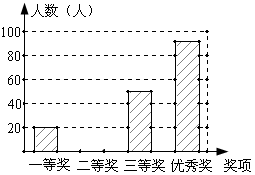
(1)一等奖所占的百分比是______;
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整;
(3)各奖项获奖学生分别有多少人?
如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.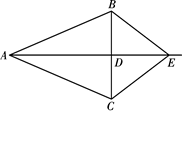
(1)求证:△ABE≌△ACE
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.