用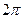
平方米的材料制成一个有盖的圆锥形容器，如果在制作过程中材料无损耗，且材料的厚度忽略不计，底面半径长为
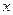，圆锥母线的长为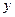
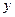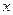（1）、建立与的函数关系式，并写出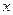的取值范围；
（2）、圆锥的母线与底面所成的角大小为
，求所制作的圆锥形容器容积多少立方米(精确到0. 01m3)
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.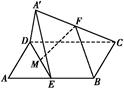
(1)求证:BF∥平面A′DE;
(2)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB=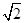
,CE=EF=1.
(1)求证:AF∥平面BDE;
(2)求证:CF⊥平面BDE.
如图,几何体E
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
如图,直三棱柱ABC
A′B′C′,∠BAC=90°,AB=AC=
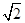,AA′=1,点M,N分别为
A′B和B′C′的中点.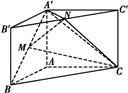
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′MNC的体积.(锥体体积公式V=
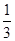Sh,其中S为底面面积,h为高)
如图,在四棱锥P
ABCD中,底面是边长为2
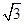的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
,M、N分别为PB、PD的中点.
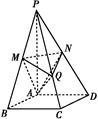
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角AMNQ的平面角的余弦值.