某工厂建造一个无盖的长方体蓄水池,其容积为4800 ,深度为3m,如果池底每1
,深度为3m,如果池底每1 的造价为150元,池壁每1
的造价为150元,池壁每1 的造价为120元,怎样设计水池的底面长与宽的尺寸才能使总造价最低?最低总造价为多少元?
的造价为120元,怎样设计水池的底面长与宽的尺寸才能使总造价最低?最低总造价为多少元?
在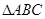 中,角A,B,C的对边分别是a,b,c,已知
中,角A,B,C的对边分别是a,b,c,已知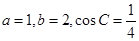
(1)求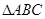 的周长
的周长
(2)求值: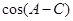 的值
的值
已知集合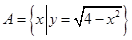 ,集合
,集合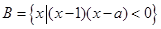 ,
,
(1)若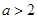 ,求
,求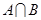
(2)若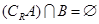 ,求实数a 的范围
,求实数a 的范围
选修4-5:不等式选讲
已知函数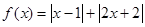
(1)解不等式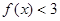 ;
;
(2)若不等式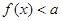 的解集为空集,求实数
的解集为空集,求实数 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程
平面直角坐标系中,已知曲线 ,将曲线
,将曲线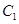 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的 倍和
倍和 倍后,得到曲线
倍后,得到曲线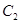
(1)试写出曲线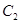 的参数方程;
的参数方程;
(2)在曲线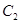 上求点
上求点 ,使得点
,使得点 到直线
到直线 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.