(本小题满分13分)如图,四棱锥 中,
中, 平面
平面
 ,
, .
.
(1)求三棱锥 的外接球的体积;
的外接球的体积;
(2)求二面角 与二面角
与二面角 的正弦值之比.
的正弦值之比.
【改编】(本小题满分12分)在 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 且
且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求△
,求△ 的周长.
的周长.
如图,在平面直角坐标系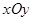 中,点
中,点 ,直线
,直线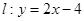 .设圆
.设圆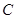 的半径为
的半径为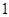 ,圆心在
,圆心在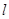 上.
上.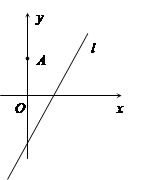
(1)若圆心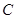 也在直线
也在直线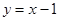 上,过点
上,过点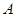 作圆
作圆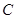 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆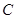 上存在点
上存在点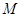 ,使
,使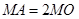 ,求圆心
,求圆心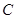 的横坐标
的横坐标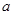 的取值范围.
的取值范围.
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面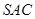 均为边长为1的等边三角形,
均为边长为1的等边三角形,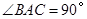 ,
,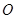 为
为 中点.
中点.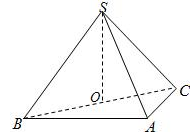
(Ⅰ)证明: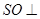 平面
平面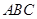 ;
;
(Ⅱ)证明: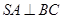 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
【改编】已知圆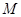 :
: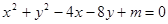 与
与 轴相切,点
轴相切,点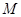 为圆心.
为圆心.
(1)求 的值;
的值;
(2)求圆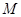 在
在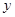 轴上截得的弦长;
轴上截得的弦长;
(3)若点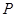 是直线
是直线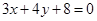 上的动点,过点
上的动点,过点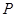 作直线
作直线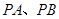 与圆
与圆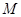 相切,
相切,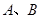 为切点.当切线长最短时,求四边形
为切点.当切线长最短时,求四边形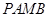 的面积.
的面积.