(本小题满分14分)已知函数 的定义域为
的定义域为 ,设
,设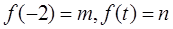 .
.
(1)试确定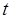 的取值范围,使得函数
的取值范围,使得函数 在
在 上为单调函数;
上为单调函数;
(2)求证: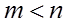 ;
;
(3)求证:对于任意的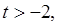 总存在
总存在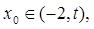 满足
满足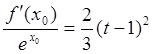 ;
;
又若方程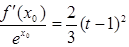 在
在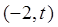 上有唯一解,请确定
上有唯一解,请确定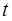 的取值范围.
的取值范围.
(本小题满分14分)
已知各项均为正数的数列 的前
的前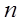 项和为
项和为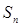 ,且
,且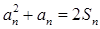 .
.
(1)求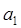 ;
;
(2)求数列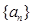 的通项公式;
的通项公式;
(3)若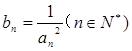 ,
, ,求证:
,求证: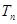 <
<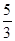 .
.
(本小题满分14分)如图,在三棱锥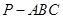 中,
中,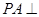 底面ABC,
底面ABC, ,AP="AC," 点
,AP="AC," 点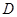 ,
,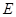 分别在棱
分别在棱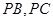 上,且BC//平面ADE.
上,且BC//平面ADE.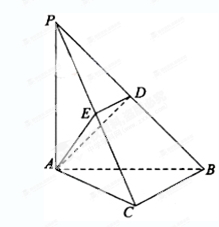
(Ⅰ)求证:DE⊥平面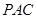 ;
;
(Ⅱ)若PC⊥AD,且三棱锥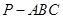 的体积为8,求多面体ABCED的体积.
的体积为8,求多面体ABCED的体积.
(本小题满分14分)设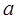 ∈R, 解关于
∈R, 解关于 的不等式
的不等式 ≥
≥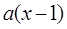 .(要求:对结果作综述,解集用区间表示)
.(要求:对结果作综述,解集用区间表示)
(本小题满分12分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
| 健康指数 |
2 |
1 |
0 |
﹣1 |
| 60岁至79岁的人数 |
120 |
133 |
32 |
15 |
| 80岁及以上的人数 |
9 |
18 |
14 |
9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,﹣1代表“生活不能自理”.
(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老龄人生活能够自理的概率是多少?
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.