（本小题满分14分）如图，在三棱锥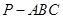
中，
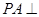底面ABC,
，AP="AC," 点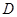
，
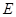分别在棱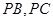
上，且BC//平面ADE.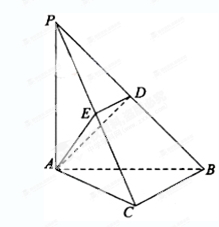
（Ⅰ）求证：DE⊥平面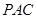
；
（Ⅱ）若PC⊥AD，且三棱锥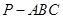的体积为8，求多面体ABCED的体积．
在△ABC中，a、b、c分别表示三个内角∠A、∠B、∠C的对边，如果(a2＋b2)sin(A－B)＝(a2－b2)sin(A＋B)，判断三角形的形状．
在△ABC中，角A、B、C所对的边分别是a、b、c，已知c＝2，C＝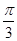
.
(1)若△ABC的面积等于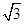
，求a、b；
(2)若sinC＋sin(B－A)＝2sin2A，求△ABC的面积．
在△ABC中，a、b、c分别是角A、B、C的对边，且
.
(1)求角B的大小；
(2)若b＝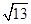
，a＋c＝4，求△ABC的面积．
在△ABC中，a＝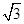
，b＝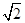
，B＝45°.求角A、C和边c.
设函数f(x)＝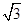
sinxcosx＋cos2x＋a.
(1)写出函数f(x)的最小正周期及单调递减区间；
(2)当x∈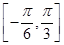
时，函数f(x)的最大值与最小值的和为
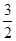，求a的值．