(
设函数
⑴若 时,解不等式
时,解不等式 ;
;
⑵如果对于任意的 ,
, ,求
,求 的取值范围。
的取值范围。
在直角坐标系
中,已知点
,点
在
三边围成的区域(含边界)上,且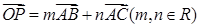
(1)若
,求
;
(2)用
表示
,并求
的最大值.
四面体
及其三视图如图所示,平行于棱
的平面分别交四面体的棱
于点
.
(1)求四面体
的体积;
(2)证明:四边形
是矩形.
的内角
所对的边分别为
.
(1)若
成等差数列,证明:
;
(2)若
成等比数列,且
,求
的值.
在平面直角坐标系
中,椭圆
的离心率为
,直线
被椭圆
截得的线段长为
.
(Ⅰ)求椭圆
的方程;
(Ⅱ)过原点的直线与椭圆
交于
两点(
不是椭圆
的顶点).点
在椭圆
上,且
,直线
与
轴、
轴分别交于
两点.
(i)设直线
的斜率分别为
,证明存在常数
使得
,并求出
的值;
(ii)求
面积的最大值.
设函数 其中 为常数,
(1)若 ,求曲线 处的切线方程;
(2)讨论函数 的单调性.
的单调性.