(本小题满分12分）
投到“时尚生活”杂志的稿件，先由两位初审专家进行评审，若能通过两位初审专家的评审，则予以录用；若两位初审专家都未通过，则不予录用；若恰能通过一位初审专家的评审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则，不予录用.设稿件能通过各初审专家评审的概率均为0.5，
复审的稿件能通过评审的概率为0.3，各位专家独立评审.
（1）求投到该杂志的1篇稿件被录用的概率.
（2）若某人投到该杂志3篇稿件，求他被录用稿件篇数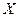
的分布列及期望值.
如图，四棱锥
的底面是正方形，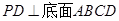
，点E在棱PB上.
（1）求证：平面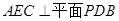
；
（2）当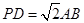
且E为PB的中点时，求AE与平面PDB所成的角的大小.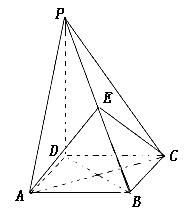
如图，在长方体ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动.
（1）证明：D1E⊥A1D；
（2）当E为AB的中点时，求点E到面ACD1的距离；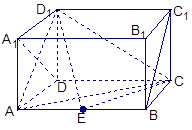
正方体ABCD－A1B1C1D1中，M，N分别是AB，A1D1的中点.
求证：MN∥平面BB1D1D．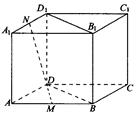
已知p:方程x2＋mx＋1=0有两个不等的负根；q:方程4x2＋4(m－2)x＋1＝0无实根．若“p或q”为真，“p且q”为假，求m的取值范围．
已知命题
“若
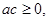则二次方程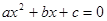
没有实根”.
(1)写出命题
的否命题； (2)判断命题的否命题的真假, 并证明你的结论.