已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
如图,要设计一张矩形广告,该广告含有左右大小相等在两个矩形栏目(即图中在阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏中间的中缝空白的宽度为5cm,问怎样设计每个栏目的宽和高,能使整张广告的面积最小?
已知数列{an}的前n项和Sn=
(1)确定常数K并求a ;
;
(2)求数列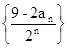 的前n项和Tn
的前n项和Tn
在 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若
(1)求角A;
(2)已知 ,求
,求 面积的最大值。
面积的最大值。
设数列 前
前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 求证
求证 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,求数列
,求数列 的前
的前 和
和 .
.
设 中的内角
中的内角 的对应边分别为
的对应边分别为 ,已知
,已知
(1)求 的边长
的边长 ;
;
(2)求 的值
的值