、已知直线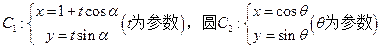 .
.
(1) 当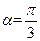 时,求
时,求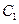 与
与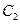 的交点;
的交点;
(2)设曲线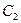 经过伸缩变换
经过伸缩变换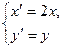 得到曲线
得到曲线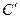 ,设曲线
,设曲线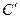 上任一点为
上任一点为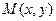 ,
,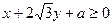 恒成立,求
恒成立,求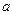 的取值范围。
的取值范围。
(本小题满分12分)直三棱柱 中,
中,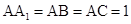 ,
,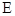 ,
,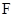 分别是
分别是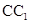 、
、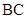 的中点,
的中点,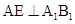 ,
,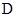 为棱
为棱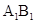 上的点.
上的点.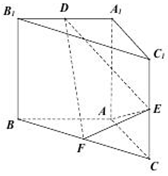
(1)证明: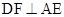 ;
;
(2)是否存在一点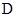 ,使得平面
,使得平面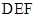 与平面
与平面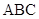 所成锐二面角的余弦值为
所成锐二面角的余弦值为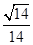 ?若存在,说明点
?若存在,说明点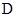 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
(本小题满分12分)甲、乙两袋中各装有大小相同的小球 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为 、
、 、
、 ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为 ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在锐角三角形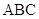 中,
中, 、
、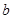 、
、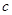 分别是角
分别是角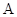 、
、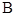 、
、 的对边,且
的对边,且 .
.
(1)求角 的大小;
的大小;
(2)若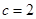 ,求
,求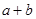 的最大值.
的最大值.
(本小题满分10分)选修4—5:不等式选讲
设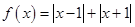 .
.
(1)求 的解集;
的解集;
(2)若不等式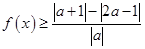 对任意实数
对任意实数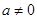 恒成立,求实数
恒成立,求实数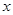 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆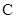 的参数方程
的参数方程 (
(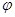 为参数).以
为参数).以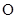 为极点,
为极点,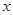 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆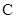 的极坐标方程;
的极坐标方程;
(2)直线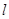 的极坐标方程是
的极坐标方程是 ,射线
,射线
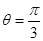 与圆
与圆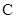 的交点为
的交点为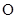 、
、 ,与直线
,与直线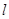 的交点为
的交点为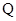 ,求线段
,求线段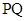 的长.
的长.