在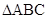 中,角
中,角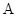 ,
,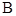 ,
, 所对的边分别为
所对的边分别为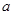 ,
,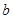 ,
,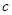 ,且满足
,且满足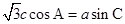 .
.
(1)若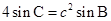 ,求
,求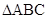 的面积;
的面积;
(2)若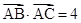 ,求
,求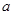 的最小值.
的最小值.
设函数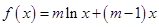 .
.
(1)若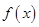 存在最大值
存在最大值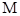 ,且
,且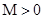 ,求
,求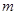 的取值范围;
的取值范围;
(2)当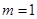 时,试问方程
时,试问方程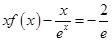 是否有实数根,若有,求出所有实数根;若没有,请说明理由.
是否有实数根,若有,求出所有实数根;若没有,请说明理由.
已知函数 .
.
(1)当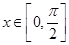 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若 ,求函数
,求函数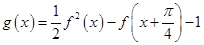 的值域.
的值域.
已知数列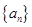 ,
,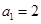 ,当
,当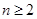 时,
时,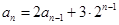 .
.
(1)求数列 及数列
及数列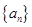 的通项公式;
的通项公式;
(2)令 ,设
,设 为数列
为数列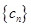 的前
的前 项和,求
项和,求 .
.
某市政府欲在如图所示的矩形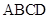 的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形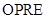 (线段
(线段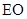 和
和 为两条底边),已知
为两条底边),已知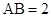
 ,
,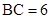
 ,
,
 ,其中曲线
,其中曲线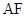 是以
是以 为顶点、
为顶点、 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
(1)求曲线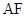 与
与 ,
,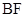 所围成区域的面积;
所围成区域的面积;
(2)求该公园的最大面积.