求证:(1) ;
;
(2)  +
+ >
>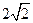 +
+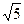 。
。
一空间几何体的三视图如图所示,求该几何体的体积。
已知函数 且此函数图象过点(1, 5).(1)求实数m的值;(2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1, 5).(1)求实数m的值;(2)判断f(x)奇偶性;(3)讨论函数f(x)在 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.
设函数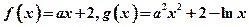 ,其中
,其中 ,
,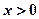 。
。
(1)若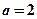 ,求曲线
,求曲线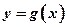 在
在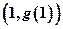 点处的切线方程;
点处的切线方程;
(2)是否存在负数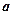 ,使
,使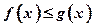 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出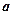 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
已知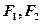 分别是椭圆
分别是椭圆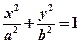
 的左、右 焦点,已知点
的左、右 焦点,已知点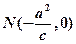 满足
满足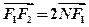 ,且
,且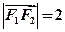 。设
。设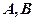 是上半椭圆上且满足
是上半椭圆上且满足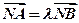 的两点。
的两点。
(1)求此椭圆的方程;
(2)若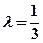 ,求直线AB的斜率。
,求直线AB的斜率。
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R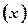 万元,且R
万元,且R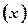
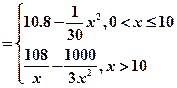
(1)写出年利润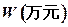 关于年产量
关于年产量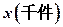 的函数解析式;
的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)