我们约定，若一个三角形（记为△A1）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A1是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1，由△A复制出△A1，又由△A1复制出△A2，再由△A2复制出△A3，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，通过复制形成的多边形中的任意相邻两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
（1）图1中标出的是一种可能的复制结果，小明发现△A∽△B，其相似比为_________．在图1的基础上继续复制下去得到△C，若△C的一条边上恰有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是________；
（3）请你用两
次旋转和一次平移复制形成一个四
边形，在图2的方框内画出草图，并仿照图1作出标记．
小明是一名升旗手，面对高高的旗杆，他想出了好几种方法测量方法，学过直角三角形后，他只用一把卷尺就测出了旗杆AB的高度．下面是他测量的过程和数据：
第一步：测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1m（如图1），
第二步：拉着绳子的下端往后退，当他将绳子拉直时，测得此时拉绳子的手到地面的距离CD为1m，到旗杆的距离CE为8m，（如图2）．他很快算出了旗杆的高度，请你也来试一试．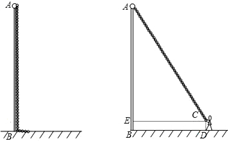
如图，AD∥BC，∠A=90°，E是AB上的一点，且AD=BE，∠DEC=90°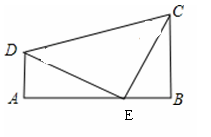
（1）△CDE是什么三角形？请说明理由
（2）若AD=6，AB=14，请求出BC的长．
如图所示，BC⊥ED，垂足为O，∠A=27°，∠D=20°，求∠ACB与∠B的度数．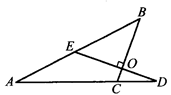
如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，请你通过尺规作图找出这一P点，（不写作法，保留作图痕迹）．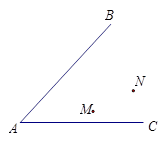
（本题12分）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E．证明:DE=BD+CE．
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角．请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由．
（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．