抛物线 ,a>0,c<0,
,a>0,c<0,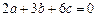 .
.
(1)求证: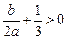 ;
;
(2)抛物线经过点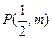 ,Q
,Q .
.
① 判断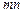 的符号;
的符号;
② 若抛物线与x轴的两个交点分别为点A ,点B
,点B (点A在点B左侧),请说明
(点A在点B左侧),请说明 ,
,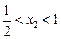 .
.
(本题满分12分)现在,友谊商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果友谊商场还能盈利25%,这台冰箱的进价是多少元?
(本题满分10分) 2013年6月11日17时18分,神舟十号载人飞船顺利升空,同学们倍受鼓舞,开展了火箭模型的制作比赛,右图为火箭模型的截面图:下面为等腰梯形,中间是长方形,上面是三角形.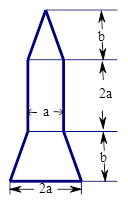
(1)请你用含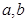 的式子表示该截面的面积
的式子表示该截面的面积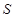 ;
;
(2)当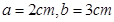 时,求这个火箭模型截面的面积.
时,求这个火箭模型截面的面积.
(本题满分10分)如图,已知线段AB=40厘米,E为AB的中点,C在EB上,F为CB的中点,且FB=6厘米,求CE的长.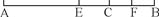
(本题满分8分)三个队植树,第一队种a棵,第二队种的比第一队种的树的2倍还少8棵,第三队种的比第二队种的树的一半多6棵,问三个队共种多少棵树?并求当 棵时,三个队种树的总棵数.
棵时,三个队种树的总棵数.
(本题满分8分)如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.
(1)请把-10,8,10,-3,-8,3分别填入六个小正方形中.
(2)若某相对两个面上的数字分别满足关系式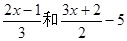 ,求
,求