（本小题满分12分）
已知函数f（x）＝
－x （e为自然对数的底数）．
（Ⅰ）求f（x）的最小值；
（Ⅱ）不等式f（x）>ax的解集为P，若M＝{x｜
≤x≤2}且M∩P≠
，求实数a的
取值范围；
（Ⅲ）已知n∈N﹡，且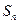
＝
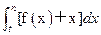（t为常数，t≥0），是否存在等比数列{
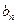}，使得b1＋b2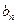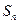＋…＝?若存在，请求出数列{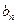}的通项公式；若不存在，请说明理由．
在平面直角坐标系xOy中，已知点A(-1, 0)、B(1, 0), 动点C满足条件：△ABC的周长为
．记动点C的轨迹为曲线W．
（Ⅰ）求W的方程；
（Ⅱ）经过点（0,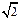 
）且斜率为k的直线l与曲线W有两个不同的交点P和Q，求k的取值范围；
（Ⅲ）已知点M（
），N（0, 1），在(Ⅱ)的条件下，是否存在常数k，使得向量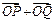
与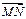
共线？如果存在，求出k的值；如果不存在，请说明理由．
数列
满足
（Ⅰ）求
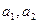的值；
（Ⅱ）记
，是否存在一个实数t，使数列
为等差数列？若存在，求出实数t；若不存在，请说明理由；
（Ⅲ）求数列{
}的前n项和Sn ．
（本小题满分12分）在一次食品卫生大检查中，执法人员从抽样中得知，目前投放我市的甲、乙两种食品的合格率分别为
和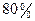
．
（1）今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率．
（2）若某消费者从两种食品中任意各购一件,设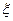
表示购得不合格食品的件数,试写出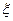
的分布列,并求其数学期望．
四边形ABCD中， BD是它的一条对角线，且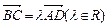
，
，
．
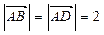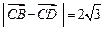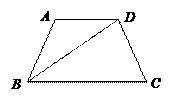
⑴若△BCD是直角三形，求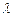
的值；
⑵在⑴的条件下，求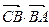
．
（本大题12分，）如图，三棱柱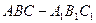
的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是，D是AC的中点。
（1）求证：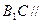
平面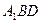
；
（2）求二面角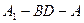
的大小；
（3）求直线
与平面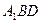所成的角的正弦值．