(本小题满分12分)在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为 和
和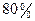 .
.
(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设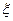 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出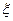
的分布列,并求其数学期望.
椭圆G: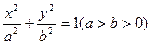 的两个焦点
的两个焦点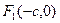 、
、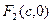 ,M是椭圆上一点,且满足
,M是椭圆上一点,且满足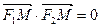 .
.
(1)求离心率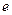 的取值范围;
的取值范围;
(2)当离心率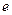 取得最小值时,点
取得最小值时,点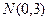 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为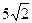 ;
;
①求此时椭圆G的方程;
②设斜率为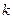 (
(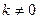 )的直线
)的直线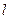 与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点
与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点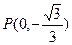 、Q的直线对称?若能,求出
、Q的直线对称?若能,求出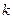 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
已知函数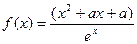 ,(
,(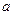 为常数,
为常数,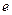 为自然对数的底).
为自然对数的底).
(1)令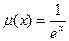 ,
,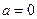 ,求
,求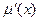 和
和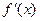 ;
;
(2)若函数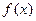 在
在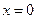 时取得极小值,试确定
时取得极小值,试确定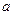 的取值范围;
的取值范围;
[理](3)在(2)的条件下,设由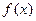 的极大值构成的函数为
的极大值构成的函数为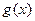 ,试判断曲线
,试判断曲线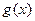 只可能与直线
只可能与直线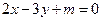 、
、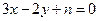 (
(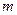 ,
,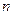 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.
[文]若数列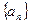 的通项公式
的通项公式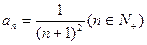 ,记
,记 .
.
(1)计算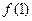 ,
,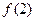 ,
,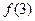 的值;
的值;
(2)由(1)推测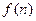 的表达式;
的表达式;
(3)证明(2)中你的结论.
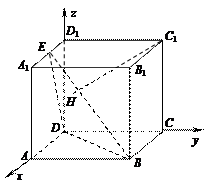
[理]如图,在正方体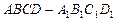 中,
中,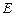 是棱
是棱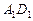 的中点,
的中点,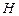 为平面
为平面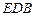 内一点,
内一点,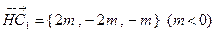 .
.
(1)证明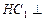 平面
平面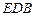 ;
;
(2)求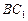 与平面
与平面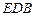 所成的角;
所成的角;
(3)若正方体的棱长为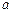 ,求三棱锥
,求三棱锥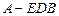 的体积.
的体积.
、设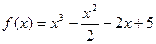 .
.
(1)求函数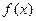 的单调递增、递减区间;
的单调递增、递减区间;
(2)求函数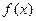 在区间
在区间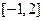 上的最大值和最小值.
上的最大值和最小值.