[理]如图,在正方体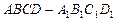 中,
中,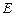 是棱
是棱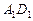 的中点,
的中点,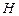 为平面
为平面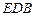 内一点,
内一点,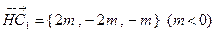 .
.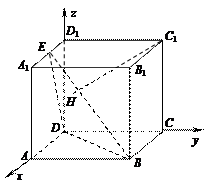
(1)证明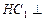 平面
平面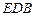 ;
;
(2)求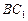 与平面
与平面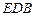 所成的角;
所成的角;
(3)若正方体的棱长为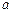 ,求三棱锥
,求三棱锥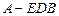 的体积.
的体积.
已知动圆M与直线y =2相切,且与定圆C: 外切,求动圆圆心M的轨迹方程.
外切,求动圆圆心M的轨迹方程.
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
请画出上表数据的散点图; (要求: 点要描粗)
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: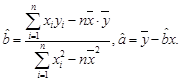 )
)
已知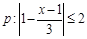 ;
; ,若
,若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数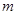 的取值范围。
的取值范围。
已知f(x)=x- (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+ )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有 成立;
成立;
(3)求证: .
.
已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.