(本小题满分13分)
随机变量X的分布列如下表如示,若数列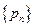 是以
是以 为首项,以
为首项,以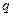 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
,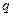 ).现随机变量X∽Q(
).现随机变量X∽Q(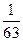 ,2).
,2).
| X |
1 |
2 |
… |
n |
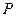 |
 |
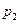 |
… |
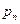 |
(Ⅰ)求n 的值并求随机变量X的数学期望EX;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变 量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
如图1,在平行四边形ABCD中,AB=1,BD= ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
(1)若F、G分别是AD、BC的中点,且AB∥平面EFG,求证:CD∥平面EFG;
(2)当图1中AE+EC最小时,求图2中二面角A-EC-B的大小.
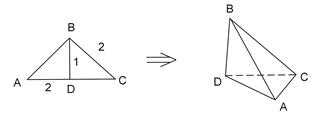
如图,在 中,
中, 为
为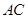 边上的高,
边上的高,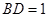 ,
,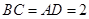 ,沿
,沿 将
将 翻折,使得
翻折,使得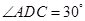 ,得到几何体
,得到几何体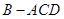 。
。
(1)求证: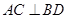 ;
;
(2)求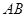 与平面
与平面 所成角的正切值。
所成角的正切值。
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中点.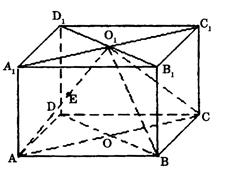
(1)求证:平面O1AC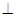 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离.
计算并输出1×2×3×4×﹣﹣﹣×n>1000的最小整数n,写出程序框图,并编写程序。
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
,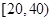 ,
, ,
, ,
, .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿;