.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(选修4—2 矩阵与变换)(本小题满分7分)
已知矩阵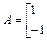
 ,向量
,向量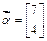 .
.
(Ⅰ) 求矩阵 的特征值
的特征值 、
、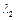 和特征向量
和特征向量 、
、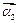 ;
;
(Ⅱ)求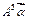 的值.
的值.
(2)(选修4—4 参数方程与极坐标)(本小题满分7分)
在极坐标系中,过曲线 外的一点
外的一点 (其中
(其中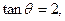
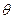 为锐角)作平行于
为锐角)作平行于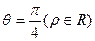 的直线
的直线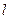 与曲线分别交于
与曲线分别交于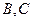 .
.
(Ⅰ) 写出曲线 和直线
和直线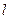 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为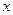 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若 成等比数列,求
成等比数列,求 的值.
的值.
(3)(选修4—5 不等式证明选讲)(本小题满分7分)
已知正实数 、
、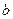 、
、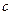 满足条件
满足条件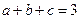 ,
,
(Ⅰ) 求证: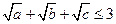 ;
;
(Ⅱ)若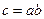 ,求
,求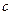 的最大值.
的最大值.
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若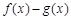 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设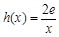 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得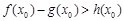 成立,求
成立,求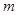 的取值范围.
的取值范围.
已知数列 满足
满足 ,且
,且 ,
,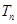 为
为 的前
的前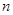 项和.
项和.
(1)求证:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)如果对于任意 ,不等式
,不等式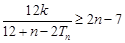 恒成立,求
恒成立,求 实数
实数 的取值范围.
的取值范围.
已知函数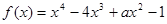 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。
(1)求 的值;
的值;
(2)若斜率为24的直线是曲线 的切线,求此直线方程;
的切线,求此直线方程;
(3)是否存在实数b,使得函数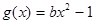 的图象与函数
的图象与函数 的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
集合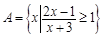 ,
,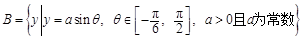 .
.
(1)求集合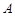 和B;
和B;
(2)若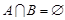 ,求
,求 的取值范围
的取值范围
已知
(1)求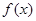 的周期,并求
的周期,并求 时的单调增区间.
时的单调增区间.
(2)在△ABC中,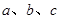 分别是角A,B,C所对的边,若
分别是角A,B,C所对的边,若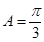 ,且
,且 ,求
,求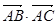 的最大值.
的最大值.