(.(本题满分12分)
已知二次函数 和“伪二次函数”
和“伪二次函数”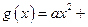
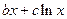 (
(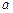 、
、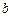 、
、
 ),
),
(I)证明:只要 ,无论
,无论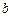 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数 图象上任意取不同两点
图象上任意取不同两点 ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 的斜率为
的斜率为 ,
,
( i)求证:
i)求证: ;
;
(ii)对于“伪二次函数” ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
(本小题满分12分)已知椭圆 ,左焦点到直线x一y一2=0的距离为
,左焦点到直线x一y一2=0的距离为 ,左焦点到左顶点的距离为
,左焦点到左顶点的距离为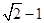 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l过点M(2,0)交椭圆于A,B两点,是否存在点N(t,0),使得 ,若存在,求出t的取值范围;若不存在,说明理由.
,若存在,求出t的取值范围;若不存在,说明理由.
(本小题满分12分)如图,四棱锥S一ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC= ,SA=SC=SD=2.
,SA=SC=SD=2.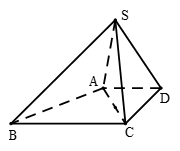
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角A - SB -C的余弦值.
(本小题满分12分)甲、乙两名射击运动员参加某项有奖射击活动(射击次数相同).已知两名运动员射击的环数都稳定在7,8,9,10环,他们射击成绩的条形图如下: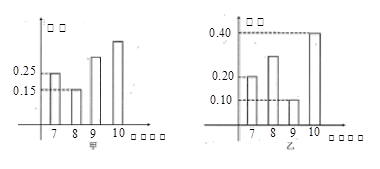
(Ⅰ)求乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率.
(Ⅱ)甲、乙两名运动员现在要同时射击4次,如果甲、乙同时击中9环以上(包括9环)3次时,可获得总奖金两万元;如果甲、乙同时击中9环以上(包括9环)4次时,可获得总奖金五万元,其他结果不予奖励.求甲、乙两名运动员可获得总奖金数的期望值.
(注:频率可近似看作概率)
(本小题满分12分)如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为α,再由点C沿东偏北β(β<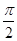 )角方向走d米到达位置D,测得∠BDC=γ.
)角方向走d米到达位置D,测得∠BDC=γ.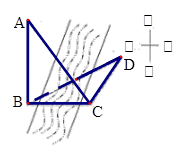
(Ⅰ)若β=75°,求sⅠn∠BCD的值;
(Ⅱ)求此建筑物的高度(用字母表示).
(本小题满分14分)已知函数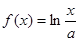 .
.
(1)若曲线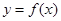 在
在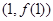 处的切线为
处的切线为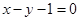 ,求
,求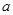 的值;
的值;
(2)设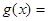
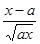 ,
,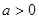 ,证明:当
,证明:当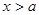 时,
时,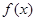 的图象始终在
的图象始终在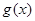 的图象的下方;
的图象的下方;
(3)当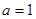 时,设
时,设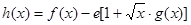 ,(
,(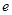 为自然对数的底数),
为自然对数的底数),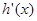 表示
表示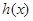 导函数,求证:对于曲线
导函数,求证:对于曲线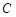 上的不同两点
上的不同两点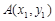 ,
,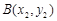 ,
,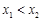 ,存在唯一的
,存在唯一的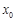
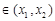 ,使直线
,使直线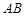 的斜率等于
的斜率等于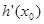 .
.