(本小题满分12分)已知 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,
轴上的双曲线, :方程
:方程 =(
=( 一
一 )
) 表示开口向右的抛物线.若“
表示开口向右的抛物线.若“

 ”为真命题,“
”为真命题,“

 ”为假命题,求实数
”为假命题,求实数 的范围.
的范围.
△ABC中,已知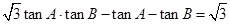 ,记角A,B,C的对边
,记角A,B,C的对边
依次为a,b,c,
(1)求∠C大小;
(2)若c=2,且△ABC为锐角三角形,求a2+b2取值范围。
12分)设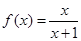 ,在由直线
,在由直线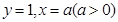 及坐标轴所围成的区域内任意
及坐标轴所围成的区域内任意
投一质点M,点M落在由曲线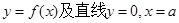 所围成的区域内概率为
所围成的区域内概率为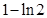 ,求
,求
a值。
直线 l 被两直线 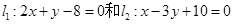 截得线段中点是M
截得线段中点是M
(0,1),求l方程。
已知函数f(x)=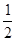 x
x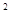 -ax+(a-1)
-ax+(a-1) ,
,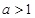 。
。
(1)讨论函数 的单调性;
的单调性;
(2)证明:若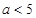 ,则对任意x
,则对任意x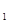 ,x
,x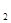
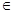
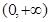 ,x
,x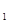
 x
x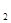 ,有
,有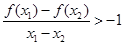 。
。
已知,椭圆C过点A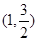 ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(1)求椭圆C的方程;
(2)E、F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。